Flat Earth Claim
The Horizon Always Rises To Eye Level
The Facts
What I want to know is, how exactly did you measure that?
It certainly does not look "eye-level" to me.
In fact, trivial observation shows that it drops by pretty much EXACTLY the amount we would expect on an Earth with a radius of approximately 3959 miles.
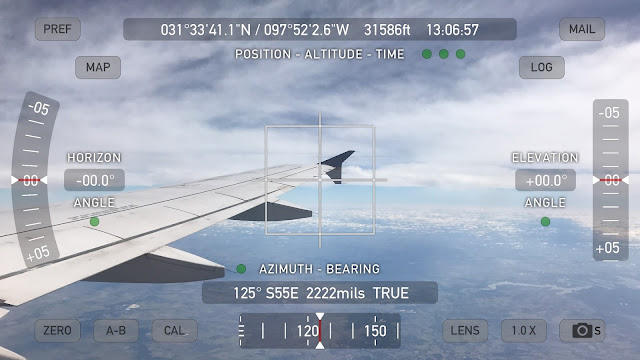
I have a Theodolite application on my iPhone 7 Plus which uses the accelerometers to position a reticle in the camera view marking out level & plumb and has indicators showing the angle of the camera in relationship to level. In the image below I have purposefully tilted the camera along two axes so you can see that the reticle has turned red indicating that my view is very tilted but it has aligned itself to the horizon while the white cross-marks simply mark center of the camera view.
So it doesn't matter if my phone or the plane or anything else is tilted, the angles indicated by the Horizon Angle and Elevation Angle indicators are relative to LEVEL.
 |
| Figure 1 |
And yes, these are from a different flight so I'm on opposite sides of different planes, at different times. I didn't think to take the above picture until my return flight but I wanted to show readers that the reticle finds LEVEL with our view regardless of what the camera is doing.
If the Earth is approximately a sphere with radius R = 3959 miles or 20903520 feet we would expect that a viewer at greater and greater heights would (using the left-side example here):
 |
| Figure 2 |
#1 see an increasingly distant horizon equal to equation (1) above where distance to the horizon (d):
- d = √h √(h+2R)
#2 that the angle down to the horizon would thus be equal to:
- horizon dip angle = arcsin(d/(R+h))
Armed with this information we can now look at two examples I captured.
Example #1
h=24854 feet
R=20903520 (Earth radius in feet)
d=1019651.849' (about 193 miles to the horizon) [wolfram|alpha]
horizon dip angle = ~2.79° [wolfram|alpha]
 |
| Figure 3 - Example 1 |
There are a few sources of error here such as clouds, particulates in the atmosphere, and refraction affecting our true horizon so we cannot make an exact measurement. Let's see if this holds...
Example #2
Now we're up much higher...
h=38805 feet
R=20903520 (Earth radius in feet)
d=1274295.105' (about 241 miles to the horizon) [wolfram|alpha]
horizon dip angle = ~3.49° [wolfram|alpha]
 |
| Figure 4 - Example 2 |
 |
| Figure 5 |
This is, IN NO WAY, "rising to eye level" - this is the exact opposite of that.
In fact, let's watch a movie showing this horizon drop in action aboard a drone:
Here is a video from the cockpit of a commercial flight showing the Horizon angle:
Here is another video on this subject:
Conclusion
Flat Earth is flat out busted - there is no excuse for such shoddy work. Anyone claiming this is either knowingly a liar or lying in the sense that they haven't actually tested it but are making the assertion AS IF they know what they are talking about, when they very clearly do not.
They are already back-peddling and making excuses.
@ColdDimSum @judekatttt @600jefe @wordofsock @grunzwanzling42 @Fuelie327 Eye level isn't correct term. A ball would get lower as u climb up.— NASA Lies (@Portland_Ghosts) October 22, 2016
Funny that you have to make excuses as to why YOUR claims fail and end up looking exactly like an oblate spheroid Earth and, as I showed, the horizon getting lower as you climb up is exactly what we observe and it lowers an amount GREATER than a flat plane would because the curvature drops off at an exponential rate the higher we get.
The angle would be trivial to calculate on a flat plane Earth because RISE/RUN would give you the slope and the inverse tangent of a slope is an angle. But Flat Earth can't even tell you why your distance increases with altitude (except by their false appeal to perspective) or by how much.
But let's try that with our second example:
rise = h = 38805'
run = d = 1274295.105'
Gives us an angle of 1.744° [wolfram|alpha] from tan⁻¹(38805/1274295.105)
So toss this on the pile of Flat Earth Failures.
2017-09-14 Follow Up on Mike F
Our friend Make F writes:
>> Lots of million dollar words and mathematical equations, is that supposed to blow us away? Are we supposed to say "wow this guy is smart he must really have this all figured out"? 1st of all, any photographer will tell you that if your camera is level, the horizon will be exactly in the middle of your shot regardless of where the shot is taken.
Funny, because I took those shots too -- now, looking at these shots, can you tell me what the angle between LEVEL and the horizon is? You can't because it isn't being measured so we would have to GUESS AT IT.
Mike F also writes:
>>> Why did you tilt your camera?
SO I COULD MEASURE THE ANGLE BETWEEN LEVEL AND WHERE THE HORIZON IS.
Do you understand now?
These images also show that NOTHING else changes except the ANGLE indicator allows us to MEASURE the angle between level and where the horizon actually is (not at eye-level).
>>> All you need to do to confirm that the horizon always rises to eye level is put your camera on a perfectly level surface and snap a picture at various heights
The Theodolite function tells us when the camera is level as I demonstrated in the first first image on this page -- REGARDLESS of the tilt or orientation of the camera the colored reticle MARKS LEVEL from our position and the Horizon & Elevation angle indicators show you how tilted you are from level in each plane.
>> Every single shot will feature the horizon in the exact middle because... the horizon always rises to eye level. What a complete waste of time your test and accompanying novel was!! Go do it again with a level angle next time genius!
That is a complete lie and I have demonstrated this repeatedly.
More importantly I've shown YOU how to do the test yourself... where are YOUR images?
While I'm here -- let's do this with a water level:
Or watch Sly's other excellent video on the subject:
Now, the REAL question here is, will you
A) Admit your error full stop?
B) Pivot and throw out some other UTTER BULLSHIT lies?
C) Crawl back under your rock?
My history with Flat Earthers suggests B. But maybe you'll surprise me.














It seems the plane is banking and the app was probably calibrated to level flight. Note the bright spot on the wing tip is isolated and if we were level the whole wing should be more consistent.
ReplyDeleteFirst of all, as the 'calibration' image on the ground shows, the app doesn't care what angle the phone or plane is at, the reticle marks out level regardless. Secondly, those images are 36 minutes apart, the plane has moved a great distance, the Earth has rotated so the Sun is in a different part of the sky and the plane isn't even necessarily pointed in the same direction. You cannot look at some spot on the wing as an indicator of 'level'. I was very careful when I took the images to make sure the plane wasn't maneuvering. The first image WAS climbing, but the image at 38,805ft is level, steady flight.
DeleteBut the good news is YOU DON'T HAVE TO TAKE MY WORD FOR IT.
As I mentioned in my earlier comment your objections are pointless because the POINT here is to give people the METHOD so they can make their own observations. If I'm lying about the method then PROVE it. What you are doing here is the same bullshit that conspiracy theorists pull - "well, MAYBE, blah blah blah". On the chance that your comment was pre-updated images I'll leave it with this as a warning.
DO YOUR OWN EXPERIMENTS. This one is deadass simple -- buy one cheap smartphone app. There is no excuse for failure to execute here except being disingenuous.
If I get a chance in the future to film a cup of water along with the observations I'll do that -- it's not necessarily easy to do that however. Meanwhile, do it yourself. That's the beauty of such simple observations, you can repeat them yourself.
So, it's been 6 months since your comment -- have you made any such observations on your own?
I captured new images with an updated version of the app and have updated and greatly expanded on this page now.
ReplyDeleteI included an image to show the calibration accuracy on the ground. I actually didn't recalibrate at all because I didn't need to - it was already accurate, I just checked it on the ground.
However, the point isn't to trust ME but to give readers METHODS where they can verify reality for themselves. Hundreds of millions of people have cameras and apps that can trivially replicate this.
I also included Sly's analysis video on the flat earther David Ray showing his drone video and CLAIMING that the horizon is rising to Eye level when it very clearly is DROPPING off. Hoisted by his own petard.
So... thank you for your feedback on the calibration question. However...
>> "Note the bright spot on the wing tip is isolated and if we were level the whole wing should be more consistent."
This is false and has zero basis in reality. The shape and relative angle to the wing would determine the pattern of spectacular reflections off the wing - the rotation of the plane would only change the relative angle from what it HAPPENED to be at that moment - which you have no information about so your assertion here is just making things up. Before you try making things up again you should be prepared to show your calculations supporting such assertions.
In future criticism please don't make things up.
Hope you like the updated page
Lots of million dollar words and mathematical equations, is that supposed to blow us away? Are we supposed to say "wow this guy is smart he must really have this all figured out"? 1st of all, any photographer will tell you that if your camera is level, the horizon will be exactly in the middle of your shot regardless of where the shot is taken. Why did you tilt your camera? All you need to do to confirm that the horizon always rises to eye level is put your camera on a perfectly level surface and snap a picture at various heights. Every single shot will feature the horizon in the exact middle because... the horizon always rises to eye level. What a complete waste of time your test and accompanying novel was!! Go do it again with a level angle next time genius!
ReplyDeleteHoly basket-of-jumping-squirrel-balls! You spastics will quite literally tell yourselves any nutty bullshit required to cling pathetically to your ticket to Insaneville. Can you provide a count of how many goddamned times this post encourages the reader to DO THE BLASTED EXPERIMENT YOUR GODDAMMED SELF! The lengths you'll go to is seriously mind-boggling. How do you manage to get your britches on without injuring yourself? Seriously though, your arbitrary requirement of starting on a level plane comes 100% directly out of reality's disabled cousin's poo-hole. Let's take a look at just how moronic your response is, shall we?
Delete"All you need to do to confirm that the horizon always rises to eye level.."
Go ahead and read over this turd of yours a few times. See if you can knuckle the stupidity out of this stupid-sandwich.. No? Try replacing "confirm that" with "artificially make", which is what your dishonest ass is ACTUALLY saying.
"1st of all, any photographer will tell you that if your camera is level, the horizon will be exactly in the middle.."
Uh... Wha..? Neither his person nor his camera is NOT starting on level surface... That.. that's the GODDAMM point, you halfwit.
"Why did you tilt your camera?"
Jesus... Did you READ the artical or were you distracted trying to fit your reading device in your ass with the rest of your ideas?
"Go do it again with a level angle next time genius!"
I have a better idea, YOU do it and report back.
Wow, quite the tantrum for someone who's not willing to do this simple test. Not having the camera perfectly level is a foolish way of doing this test! Make the camera level and the horizon will stay PERFECTLY IN THE MIDDLE from here to as high as we can go. That will prove the flat earthers claim, not his moronic, "but I used a lot of words" test.
Delete>> quite the tantrum for someone who's not willing to do this simple test
DeletePlease share where YOU tested this yourself in a way that is verifiable and repeatable.
For example, verifiable mine uses the sensors in the phone to indicate LEVEL very clearly and I showed that it is accurate, regardless of the orientation of the device.
For Repeatable, I have done it several times and I am, in fact, repeating the tests others have done and getting the same result. I'm using nothing more than an iPhone with the Theodolite app installed which makes this TRIVIAL for anyone to repeat. And in fact, MANY have.
https://twitter.com/doctorbuttons/status/902628063908900865
https://twitter.com/wichor/status/905772452353073152
https://twitter.com/dwolfman54/status/901963727481827329
https://twitter.com/FlatSlugbrains/status/900757665550397442
https://twitter.com/FakeAstropix/status/898911034143932416
https://twitter.com/Nutt007/status/907388860145037312
https://twitter.com/Zaephou/status/900748283806613507
The Drop of the horizon with altitude has been known and measured since ANCIENT times:
https://flatearthinsanity.blogspot.com/2016/09/how-al-biruni-calculated-circumference.html
So now what are you going to do?
Let me guess -- you are going to pivot and say "well I didn't mean you could ACTUALLY SEE IT RISING cuz atmospheric density lensing perspective"?
Yet, the higher we go the FURTHER we see -- so it seems the atmosphere doesn't work the way flerfers invent in their head to excuse every failure.
I suggest you read up on refraction: http://aty.sdsu.edu/explain/atmos_refr/bending.html
and then come back when you have PROVEN that any set of likely conditions explain the actual observations other than the Earth surface is curved as we've known for thousands of years.
BTW, "rises to eye level" is a bit of a misnomer. It's more that it rises WITH eye level and not so much TO eye level. If we were on a ball the horizon would "fall away" not rise to. Make your camera perfectly level and you'll learn something new. It won't change your mind bc it's already made up, but you'll witness the phenomena.
ReplyDeleteFunny because I took those pictures -- see updated post (I added about 13 of them). I address your post in detail and shared the images in question, and I linked to two more videos that utter demolish your claims.
DeleteDude, the earth is flat no matter how much pseudoscience you impress yourself with. It's laughable how bad u want to live on a spinning ball. Get a grip.
ReplyDelete